＜私が螺旋面を選んだ理由＞

対照的な形でねじれ具合がきれいだったので選びました。

すべり台のように滑り降りたら気持ち良さそうだなと思いました。

＜螺旋面について＞

曲線Ｃが一定の角速度で回転しながら定直線Lの方向へ進むときに作る曲面

を螺旋面（helicoidal surface）という。

特にＣとLとが直交しているときにできる曲面を常螺旋面（right helicoid）という。

常螺旋面は線織面（ruled surface）で同時に極小曲面（minimal surface）

でもあるが、逆に線織面で極小曲面であるのは常螺旋面だけに限る。

＜線織面と極小曲面について＞

線織面とは、一つのパラメーターに依存する直線の族によって作られる曲面、

つまり直線が空間のなかを動くことによって得られる曲面の事である。

極小曲面とは平均曲率が至るところで０である曲面のことである。

＜等長変形について＞

懸垂面を等長変形すると常螺旋面が得られる。この変形は懸垂面に一本の母

線に沿った切れ目を入れてねじるようにして各母線が直線になるまで変形する

ことで実現する。

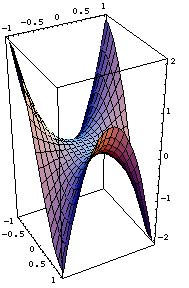
初めてこの図形を見たとき、きれいな形だと思い選びました。特に、図形の繊細さと猿の腰掛けという名前のおもしろさにひかれました。

双曲放物面とMonkey saddleは同種の曲面の有名な２つです。そして双曲放物面は、saddle surfaceと呼ばれます。それは、足のためのくぼみがあり、人が快適に座れる形だからです。しかし、しっぽをおく場所がないから猿には適していません。一方で、Monkey Saddleはその名の通り、しっぽのための場所もあり猿が座るにちょうど良い形となっています。

そして、その式は、

monkeysaddle［u＿，v＿］：={u，v，u＾３-３u v＾２}

で表されます。

また、Mathematicaでは、

ParametricPlot３D[Evaluate[Monkeysaddle[u，v] ]，{u，-１，１}，{v，-１，１}]

のように入力すれば曲線の概形を描けます。

　わたしが、この曲面を選んだ理由は、見た目が単純で分かりやすそうだし、実際にありそうで、親しみ深く感じたからです。なんとなく柔らかそうでこの中に包み込まれたいと思いました。

　この曲面について調べることにして、まず、言葉の意味から調べなければなりませんでした。

Constant Positive Curvature Surface of Revolution of the Barrel Type

一定の　　　正の　　　曲率　　　　面　　　　　回転　　　　　　　樽型

　つまり、正の定曲率回転面、そのうちの、私が選んだのは樽型の曲面です。

　ここでいう曲率とは，ガウス曲率のことです。

　ガウス曲率Kは，主曲率ｋ1、ｋ2(法曲率の最大と最小)の積であり、

Ｋ = k1・k2

と表されます。
　ガウス曲率が一定であるということは、曲面のある点における曲がり方を調べて、曲がり方の最大な方向と最小な方向の曲率をかけあわせたとき、その値が、曲面のどの点においても同じであるということです。だから、ガウス曲率が一定といった場合、一見全く違う曲がり方をしている部分があったとしても、曲がり方の最大と最小の値の積が等しいだけでよいということです。

　つぎに、ガウス曲率が正であるということについて考えてみると、主曲率k1とk2は、

k1・k2 > 0

という条件が必要です。ｋ1とｋ2は、両方が正であるか、両方が負であるかのどちらかでなくてはならず、このため、法曲率に0を含むことはできません。
　

　具体的に、曲面があり、その曲面上に自分が立っているとした場合を考えてみることにします。ｋ1＜0かつｋ2＜0ということは、その位置から、曲面上を移動しようとすると、どの方向に移動しても坂を上ることになります。逆に、ｋ1＞0かつｋ2＞0ということは，どの方向に移動しても坂を下ることになります。同じ曲面でも，その内側に立つか，外側に立つかによって，曲率が正になるか、負になるか決まることになりますが、ガウス曲率は同じです。また、その点に曲がり方が急な方向があるとしたら、必ず緩やかな方向もあるというような曲面です。さらに、回転面であるため、X-Y平面に平行に切ったら、その切り口は必ず円になるようなものと考えられます。　

　このような曲面は、ガウス曲率を正の定数とすると、次のようにパラメータ表示することができます。

　ここで、定数ｂ＞0に対して、

　　　ｂ＝ａ　ならば　球面

　　　ｂ＜ａ　ならば　フットボールのような形

　　　ｂ＞ａ　ならば　樽型

になります。ｂ>ａ場合、回転軸に交わることはなく、ａに比べてｂがそれほど大きくなければ、できあがる曲面は樽に似た形になります。

　ａ，ｂの値をいろいろ変えて表示してみることにします。

　同じ性質をもつ曲面でも、値を少し変えるだけで、全く違う曲面に見えることもあります。